Quicksort – sortowanie szybkie

Sortowanie szybkie lub zwane poprostu z angielskiego Quicksort to algorytm w którym dzięki odpowiedniej dekompozycji osiągnięto znaczący zysk szybkości sortowania. Został wynaleziony w 1962 roku przez C.A.R. Hoare’a

Procedura sortowania dzieli się na trzy główne części:

• podziału elementów tablicy względem wartości określonej komórki tablicy, służącej za oś (ang. pivot) podziału
• sortowanie podtablic przy użyciu rekurencji
• połączenia posortowanym podblic w całość

Podział

Algorytm wykorzystuje metodę dziel i zwyciężaj. W związku z tym, na samym początku odczytuje się wartość elementu osiowego (pivot), którym zazwyczaj jest pierwszy element tablicy. Może to być również element ostatni, środkowy, losowy lub inny wybrany w zdefiniowany sposób. Następnie przesuwamy mniejsze elementy tablicy na lewo, a większe lub równe na prawo. W ten sposób powstają dwie podtablice (gdzie normalnym jest, że mają różny rozmiar).

Quicksort

Kolejnym etapem algorytmu jest rekurencyjne zaaplikowanie procedury Quicksort na obu fragmentach tablicy (lewym oraz prawym) powstałych podczas podziału. Wywołania rekurencyjne zatrzymają się w momencie, gdy fragment tablicy będzie miał rozmiar 1 lub będzie pusty.

Łączenie

Końcowym elementem algorytmu jest złączenie obu fragmentów tablic oraz elementu osi podziału (lewa podtablica + oś podziału + prawa podtablica). W efekcie otrzymamy posortowaną tablicę.

Poniższa grafika przetstawiająca działanie algorytmu sortowania szybkiego:

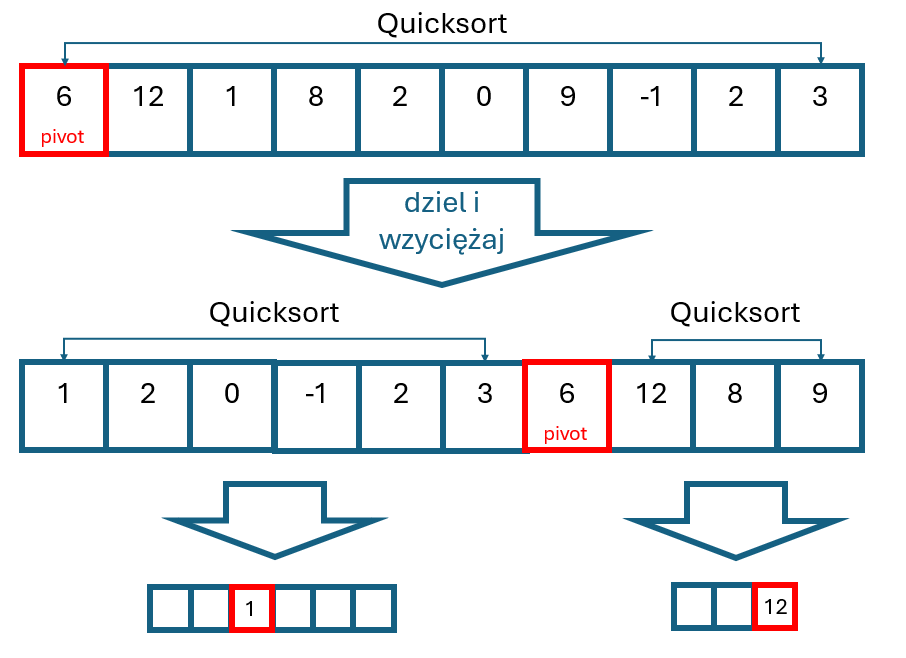
Implementacja algorytmu w Pythonie:

# funkcja rekurencyjna quicksort
def quicksort(arr):
    if len(arr) <= 1:
    	# nie ma już co dzielić i sortować
        return arr
    else:
    	# ustaw pierwszy element tablicy jako oś podziału
        pivot = arr[0]
        # elementy mniejsze od osi podziału (lewa część tablicy)
        left = [x for x in arr[1:] if x < pivot]
        # elementy większe od osi podziału lub równe (prawa część tablicy)
        right = [x for x in arr[1:] if x >= pivot]
        # połączenie posortowanych podtablic oraz osi podziału w całość
        return quicksort(left) + [pivot] + quicksort(right)
    
array_to_sort = [6, 12, 1, 8, 2, 0, 9, -1, 2, 3]
print(quicksort(array_to_sort))

Zalety algorytmu:

• złożoność czasowa: O(n log n)
• brak dodatkowej tablicy do posortowania jak to jest w przypadku sortowania przez scalanie
• łatwy w implementacji

Wady algorytmu:

• w sytuacji pesymistycznej złożoność może wynosić: O(n²)
• jest niestabilny