Najkrótsza ścieżka między dwoma węzłami grafu

Najkrótsza ścieżka w grafie pomiędzy dwoma wierzchołkami to ścieżka o minimalnej ilości krawędzi spośród dostępnych ścieżek prowadzących pomiędzy tymi wierzchołkami.

Znalezienie najkrótszej ścieżki polega na użyciu kolejki i odwiedzeniu każdego sąsiadującego węzła zaczynając od węzłów początkowych, które przemierzają graf metodą przeszukiwania wszerz, aby znaleźć najkrótszą ścieżkę między dwoma węzłami grafu. W tym celu wykorzystuje się algorytm BFS (ang. Breadth-first search).

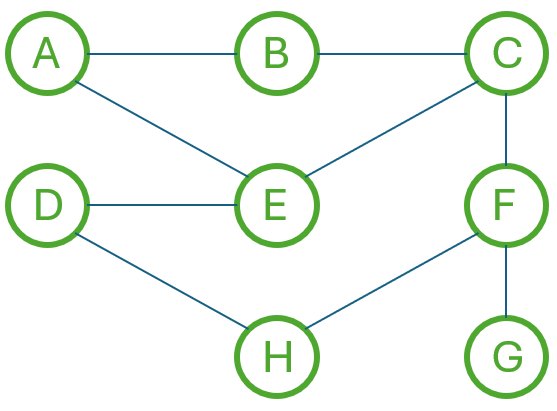
Implementacja algorytmu wyszukiwania najkrótszej ścieżki w grafie nieskierowanym z wykorzystaniem słównika reprezentującego powyższy graf:

# Funcja wyszukująca w szerz najkrotszą sciezkę pomiędzy dwoma węzłami
def bfs_sp(graph, start, end):
    explored = []
     
    # Kolejka do przejścia przez graf w BFS
    queue = [[start]]
     
    # Sprawdzenie czy węzeł początkowy i konńcowy nie są tożsame
    if start == end:
        print("Wezel poczatkowy = Wezel koncowy")
        return
     
    # Pętla do przechodzenia przez graf za pomocą kolejki
    while queue:
        path = queue.pop(0)
        node = path[-1]
         
        # Warunek sprawdzający, czy bieżący węzeł nie został odwiedzony
        if node not in explored:
            neighbours = graph[node]
             
            # Pętla umożliwiająca iterację po sąsiadach węzła
            for neighbour in neighbours:
                new_path = list(path)
                new_path.append(neighbour)
                queue.append(new_path)
                 
                # Warunek sprawdzający, czy węzeł sąsiedni jest węzłem docelownym
                if neighbour == end:
                    print("Najkrótsza ścieżka = ", *new_path)
                    return
            explored.append(node)
 
    # Informacja o stanie w którym węzły nie są połączone
    print("Ścieżka pomiędzy węzłami nie istnieje!")
    return


if __name__ == "__main__":
     
    # Graf w formie słownika wezłów
    graph = {
    	'A': ['B', 'E'],
    	'B': ['A', 'C'],
    	'C': ['B', 'E', 'F'],
    	'D': ['E', 'H'],
    	'E': ['A', 'C', 'D'],
    	'F': ['C', 'G', 'H'],
    	'G': ['F'],
    	'H': ['D', 'F']
    }
     
    # Wywołanie funkcji
    bfs_sp(graph, 'A', 'H')

Powyższy kod wyszukuje najkrótszą ścieżkę pomiędzy węzłami A oraz H.

Wygląda ona następująco: A E D H.